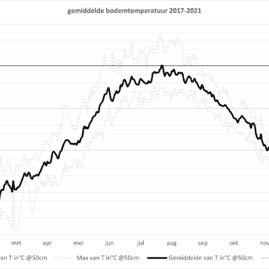
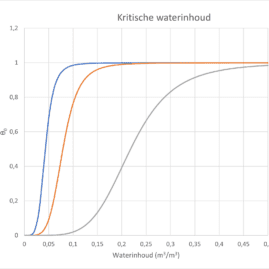
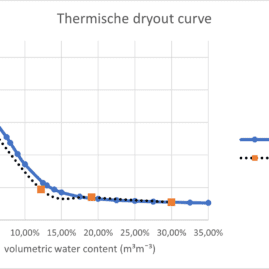
Wanneer er elektriciteit door een geleider stroomt zal dit warmte veroorzaken. Elke weerstand van de warmtestroom tussen de kabel en de grond waar deze in ligt zal zorgen dat de temperatuur van de kabel verder stijgt. Wanneer kabels worden begraven zal de grond een deel van de thermische weerstand vormen. De thermische eigenschappen van de bodem zijn daarom een belangrijk onderdeel van de dimensionering van de kabels. De theorie achter het herleiden van de warmteweerstand zie je hier onder uitgelegd.
De soortelijke warmteweerstand van de grond is het omgekeerde van thermische geleidbaarheid van de grond.
De thermische weerstand kan genoemd worden met verschillende eenheden.
Internationaal wordt gerapporteerd in SI-eenheden als °K.m/W (graden Kelvin * meter per Watt). In
het buitenland werkt men vaak met °C.cm/W (graden Celsius * centimeter per Watt).
De theorie: Hoe meten wij de thermische weerstand van grond?
Thermische geleidbaarheid (K) en soortelijke weerstand (R) kan worden gevonden door het meten van de dissipatie van een warmtebron. De vergelijking voor radiale warmtegeleiding in een homogeen, isotroop medium wordt gegeven door:
\frac{\partial T}{\partial t}
= k
\left(
\frac{\partial T}{\partial r^2} +r^{-1} \frac{\partial T}{\partial r}
\right)
\tag {1}
Waarbij T de temperatuur (°C) is, t de tijd (s), κ de thermische diffusie (m² s-1) en r de radiale afstand (m) is. Wanneer een lange, elektrisch verwarmde sonde in een medium wordt ingebracht, dan is temperatuurstijging vanaf een begintemperatuur, T0, op enige afstand, r, van de sonde:
T - T_0
=
\left(
\frac{q}{4 \pi \lambda_h} \right) E_i
\left(
\frac{-r²}{4 k t} \right)
\tag {2}Waarbij q de warmte is die wordt geproduceerd per lengte-eenheid per tijdseenheid (W m-1), λh is de thermische geleidbaarheid van het medium (W m-1C-1) en Ei is de exponentiële integrale functie.
-E_i(-a )=
\int^\infty_a
\left(
\frac{1}{u} \right) exp(-u) du =
\tag {3a} - \gamma-ln
\left(
\frac{-r²}{4 k t} \right)
+
\frac{-r²}{4 k t}
+
\left(
\frac{-r²}{8 k t} \right)
+...
\tag {3b}
Met a = r2 /4κt en γ is de constante van Euler (0,5772…). Wanneer t groot is, kunnen de hogere orde termen genegeerd worden. Wanneer wij de vergelijkingen 2 en 3 combineren dan krijgen wij:
T-T_0 \cong
\frac{q}{4 \pi \lambda_h}
\left(
ln(t)- \gamma- ln\left( \frac{r²}{4k} \right)
\right)
\tag {4}Uit de relatie tussen thermische geleidbaarheid en ∆T = T – T0, weergegeven in vergelijking 4, blijkt dat ∆T en ln(t) lineair gerelateerd zijn met een helling m = (q/4πλh). Lineaire regressie van ∆T op ln(t) levert een helling op die de thermische geleidbaarheid geeft als:
\lambda_h \cong
\frac{q}{4 \space \pi \space m}
\tag {5}Waar q het vermogen is dat aan het verwarmingselement is geleverd.
opmerking:
Om met deze methode thermische geleidbaarheid te vinden, moet worden aangenomen dat:
- Lange warmtebron kan worden gezien als een oneindig lange warmtebron
- Het medium is zowel homogeen als isotroop
- Het monster heeft een uniforme begintemperatuur T0
Hoewel het in de praktijk onmogelijk is dat al deze variabelen strikt waar zijn, is onze thermische geleidbaarheidssensor zo ontworpen dat nauwkeurige thermische geleidbaarheidsmetingen kunnen worden verkregen.
Berekeningen
De sensortemperatuur (T) tijdens verwarming wordt beschreven door:
T =
\left(
\frac{q}{\left(4 \pi k\right)} \right)
ln(t+ t_0)+C
\tag {6}Waarbij q het vermogen is (W/m), k is de thermische geleidbaarheid, t is tijd, to is een kleine tijd offset en C is een constante.
Deze vergelijking kan worden aangepast aan de gegevens van T versus t door niet-lineair regressie om k, to en C te vinden.
Een benaderingsmethode is om aan te nemen dat to = 0.
Dan is bovenstaande vergelijking lineair in ln(t). Regressie van T op ln(t) geeft een helling, s, en een snijpunt, c.
Thermische geleidbaarheid, k, wordt berekend uit de helling:
k =
\frac{q}{\left(4 \pi s\right)}
\tag {7}Aan de hand van bovenstaande theorie hebben wij een meetapparaat ontwikkeld en de software ontwikkeld waarmee wij de thermische weerstand en thermische geleidbaarheid kunnen berekenen.
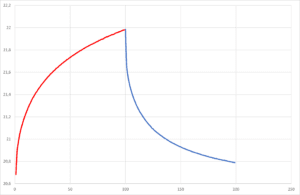
Bovenstaande grafiek laat het verwarmen van de sensor zien in rood. De kleur blauw is de gemeten temperatuur na uitschakelen van het verwarmingselement. Dit is de helling die in de bovenstaande theorie is beschreven.
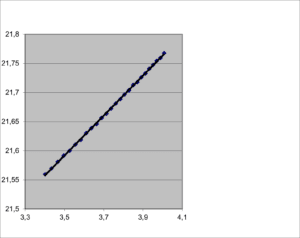
Aan de hand van de hellingshoek van de gemeten temperaturen kunnen wij de thermische weerstand afleiden.